Physik kurz und bündig

Subtraktion von Schalldruckpegeln

Im Beitrag 65 wurde bereits erörtert, dass es beim Hörempfinden des Menschen – bedingt durch Störschall (64, 65) – eine Mithörschwelle (64, 65) gibt. Störschall wird häufig auch als Hintergrundgeräusch bezeichnet. Bei Schallmessungen kann es vorkommen, dass dieses Hintergrundgeräusch die zu messende Schallquelle „übertönt“, was dazu führt, dass die Schallquelle nicht mehr gemessen werden kann. Eine Regel für die Praxis des Technikers:

Eine Schallquelle ist noch messbar, wenn der Gesamtschalldruckpegel L_p(S+H) mindestens 3 dB höher ist als der Schalldruckpegel des Hintergrundgeräusches L_pH.

S: zu messende Schallquelle

H: Hintergrundgeräusch (Störschall)

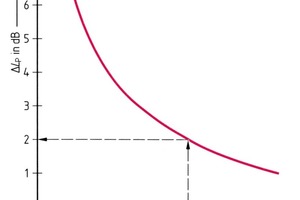
Eine Subtraktion von Schalldruckpegeln kann mit Hilfe der im Bild 1 dargestellten Kurve erfolgen, denn eine Subtraktion nach den Regeln der Arithmetik ist wegen des logarithmischen Verhältnisses bei der Berechnung des Schalldruckpegels nicht möglich.

Soll nun durch Messung der Schalldruckpegel einer Schallquelle L_pS, z.B einer laufenden Maschine, ermittelt werden, dann wird mit Hilfe des Bildes 1 wie im Schema unten auf dieser Seite vorgegangen. Ein Beispiel ist in der Musteraufgabe 1 (oben auf der nächsten Seite) wiedergegeben. Diese Musteraufgabe entspricht dem eingezeichneten Beispiel im Bild 1.

Musteraufgabe 1:

Musteraufgabe 2:

Addition von Schalldruckpegeln

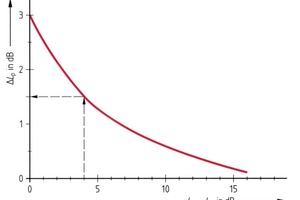
Sind die Schalldruckpegel von mehreren Schallgebern bekannt, dann  können  diese zu einem Gesamtschalldruckpegel L_pges zusammengefasst werden. Diesen bezeichnet  man auch als den resultierenden Schalldruckpegel. Wegen der logarithmischen Funktion der Einzelschalldruckpegel können diese – ebenso wie bei einer Pegelsubtraktion – nicht durch eine arithmetische Summe zusammengefasst werden. Auch hier hilft ein Diagramm (Bild 3). Am Beispiel von zwei Schallgebern, z. B. zwei laufenden Maschinen, soll die Pegeladdition, entsprechend Bild 3, erklärt werden:

1. Schalldruckpegel der einzelnen Maschinen L_p1 und L_p2 getrennt messen.

2. Differenz dieser Einzelpegel (L_P1 – L_p2) bilden. Diese ist auf der Abszisse vorzufinden.

3. Diese Pegeldifferenz liefert – entsprechend dem im Bild 3 eingezeichneten Beispiel – über die Kurve ein DL_p  auf der Ordinate.

4. Die Summe aus dem größten Einzelschalldruckpegels L_pmax und DL_p ergibt L_pges.

Somit:

Gesamtschalldruckpegel 

L_pges = L_pmax – ∆L_p

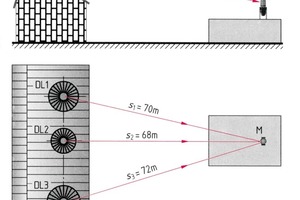
Dieses Verfahren kann auch bei mehr als zwei Schallgebern angewendet werden. In einem solchen Fall werden zunächst zwei Schallgeber zusammengefasst und fortan wie eine Schallquelle behandelt, die dann mit dem nächsten Schallgeber zusammengefasst wird. Dieses Verfahren soll mit Musteraufgabe 2 verdeutlicht werden.

Arbeiten mehrere Schallgeber gleicher Lautstärke zusammen, dann kann die Pegeladdition mit Hilfe der folgenden Tabelle erfolgen:

Verhalten des Schalls in geschlossenen Räumen

Grundsätzlich muss in der Akustik zwischen dem Schallfeld im Freien (64,65) und dem Schallfeld in geschlossenen Räumen unterschieden werden.

Das Schallfeld in geschlossenen Räumen

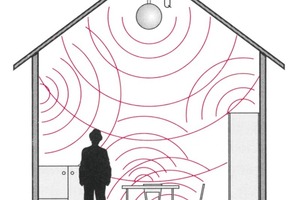
Im Freien kann sich Schall in den meisten Fällen in großen Bereichen ungehindert ausbreiten. Dieses Freifeldverhalten (64,65) ist in einem geschlossenen Raum so gut wie nicht vorzufinden. Bild 4 zeigt, dass die von einer Schallquelle Q ausgehenden Schallwellen nach kurzen Wegen auf Wände und Gegenstände treffen. Dort werden sie absorbiert, größtenteils aber reflektiert. Dies hat zur Folge, dass ein Diffusfeld (65) entsteht:

In einem Raum ist es also so, dass der Schallempfänger, z. B. das Gehör des Menschen, direkt sowohl vom Schallgeber ausgehende als auch reflektierte Wellen empfängt.

Das Schallfeld in geschlossenen Räumen ist in der Regel ein Diffusfeld.

Der Schallabsorptionsgrad

Gemäß der Beiträge 64 und 65 muss bei der Schallausbreitung die Absorption, die Reflektion, die Transmission und die Dissipation des Schalls berücksichtigt werden.
Aus dem bisher Gesagten ergibt sich, dass für die Schallempfindung in einem Raum das Verhältnis von absorbierter und reflektierter Schallenergie eine ausschlaggebende Rolle spielt. Eine Aussage hierrüber liefert die folgende aus Beitrag 65 bekannte Gleichung.

Sie lautet:

α +ρ = 1:    ρ = Schallreflektionsgrad

Somit ergibt sich für den

 
Schallabsorptionsgrad α = 1 – ρ

Der Schallabsorptiondgrad α gibt den Anteil der absorbierten („geschluckten“) Schallenergie an.

Nach Beitrag 65 setzt sich dieser Anteil an absorbierter Schallenergie aus transmittierter und dissipierter Schallenergie zusammen, und nach vorstehender Gleichung ergeben sich aus der Addition von reflektiertem und absorbierten Anteil 100 %.

Eine Wandfläche, die die ankommenden Schallwellen vollkommen absorbieren würde, hätte somit den Schallabsorptionsgrad α = 1, und man bezeichnet eine solche Wand als schallweich. Im Gegensatz hierzu gibt es die schallharte Wand, die den Schall vollkommen reflektiert. An einer solchen wäre α = 0. Beide Fälle sind idealisiert gedachte Grenzfälle. In der Praxis liegen die α-Werte zwischen etwa 0,02 und 0,45.

Im nächsten Beitrag 67 wird nochmals weitergehend auf die Begriffe schallhart und schallweich eingegangen.

In der folgenden Tabelle sind einige Durchschnittswerte von Schallabsorptionsgraden bestimmter Wandarten angegeben. Diese werden durch die Verwendung entsprechender Schalldämmstoffe erreicht. Näheres hierzu vermittelt ebenfalls der nächste Beitrag 67. Aus bautechnischen Handbüchern sind bei Bedarf weitere Werte zu erfahren.

Hinsichtlich der Raumakustik erlaubt der beschriebene Sachverhalt den folgenden Rückschluss:

Eine akustische Wandbeschreibung gilt nur für eine bestimmte Stelle in einem bestimmten Raum.

 
Für eine gute Hörsamkeit eines Raumes sind also vor allem Reflexion und Absorption an den Begrenzungsflächen des Raumes und an den im Raum befindlichen Gegenständen maßgebend. Auch auf derlei Sachverhalte wird im nächsten Beitrag 67 nochmals eingegangen.

Bilder und Daten aus Horst Herr:
„Tabellenbuch Wärme·  Kälte·  Klima“
Verlag Europa-Lehrmittel (Nr. 1731 X)
„Schwingungen und Wellen“ (Nr. 5181 X)
„Technische Physik“ (Nr. 5231 X)