Physik kurz und bündig
RaumakustikHörsamkeit
Im Beitrag 66 wurde bereits erörtert, dass eine gute Hörsamkeit – man könnte diesen Begriff auch als Qualität eines Schallereignisses deuten – vom Schallabsorptionsgrad α bzw. vom Schallreflektionsgrad ρ abhängig ist. Die Summe dieser beiden Größen hat den Wert 1 und die Größen selbst werden im Versuch ermittelt.
Die angestrebte Hörsamkeit ist immer vom Nutzungszweck des betrachteten Raumes abhängig, und eine gute Hörsamkeit ergibt sich bei den in folgender Tabelle und bereits im Beitrag 66 genannten α-Werten:
Für eine gute Hörsamkeit eines Raumes sind also vor allem Reflektion und Absorption an den Begrenzungsflächen und an den im Raum befindlichen Gegenständen (66), z. B. Möbel, Teppiche oder Vorhänge maßgebend. Wände mit besonderem akustischen Verhalten werden als Akustikflächen und Räume mit besonderem akustischen Verhalten als Akustikräume bezeichnet. In solchen müssen ,,Brennpunkteffekte“ vermieden werden, die infolge gekrümmter Wände durch Schallbündelungen entstehen können. Die wichtigste Regel für einen Raumakustiker lautet also:
Durch möglichst große Diffusität der Schallwellen an den Begrenzungsflächen eines Raumes entstehen an allen Raumpunkten annähernd gleiche Schalleindrücke.
Das akustische Verhalten von Räumen liegt in der Praxis zwischen dem akustischen Verhalten zweier Grenzfälle, nämlich dem schalltoten Raum und dem Hallraum.
Schalltote Räume
und Hallräume
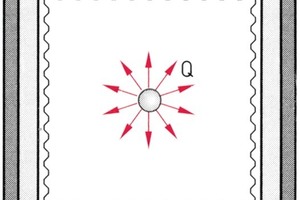
Soll der Schalldruckpegel Lρ (62, 63, 66) der Schallquelle in jeder Richtung konstant sein, z. B. bei Schallmessungen, dann muss sich die Schallquelle Q entweder in einem Freifeld (65, 66) oder in einem schalltoten Raum befinden. Ein solcher ist in Bild 1 dargestellt:
Es ist zu erkennen, dass Reflektionen dadurch vermieden werden, dass die Wände mit Schalldämmstoffen ausgekleidet sind. Es handelt sich also um schallabsorbierende Wände. Solche werden z. B. in Tonstudios realisiert, um jeglichen Störeinfluss durch Reflektionen auszuschalten.
Schalltoter Raum α = 1
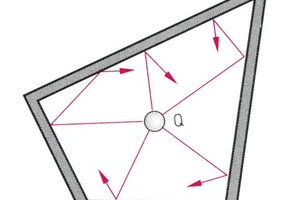
Völlig entgegengesetzt zum schalltoten Raum ist das akustische Verhalten des Hallraumes. In einem solchen sind alle Wandoberflächen so hart und reflektierend wie möglich gebaut, und es gibt darin keine parallelen Wände. Dies zeigt Bild 2:
Hallraum ρ = 1; α = 0
In einem solchen Hallraum wird von der Schallquelle Q ein völlig diffuses Schallfeld (62, 66), in dem die Schallenergie gleichmäßig verteilt ist, erzeugt. In derlei ausgeführten Räumen ist es möglich, die gesamte Schallleistung (63) des Schallgebers aus dem Schalldruckpegel an einem oder wenigen Messpunkten zu bestimmen. Die Zusammenhänge zwischen Schallleistung und Schalldruck werden noch in diesem Beitrag 67 und dem anschließenden Beitrag 68 erörtert.
Die äquivalente
Absorptionsfläche einer Wand
Denkt man sich die Fläche einer Wand aufgeteilt in einen „absolut reflektierenden“ und einen „absolut absorbierenden“ Anteil, dann nennt man den absolut absorbierenden Flächenanteil die äquivalente Absorptionsfläche Aeq.
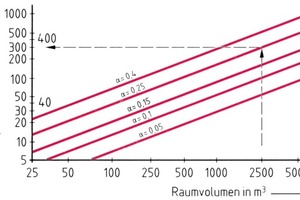
Bild 3 zeigt eine Möglichkeit zur Ermittlung derselben, wenn alle Wandinnenflächen den gleichen Wandaufbau haben, und zwar in Abhängigkeit vom Schallabsorptionsgrad α und dem Raumvolumen V.
Bei z. B. α = 0,25 und V = 2500 m3 ist (gemäß eingezeichnetem Beispiel) Aeq = 300 m2. Dieses grafische Verfahren erlaubt es lediglich, den Wert Aeq näherungsweise zu bestimmen. Entsprechend der obigen Definition ist aber die folgende Berechnung möglich:
Äquivalente Absorptionsfläche
Aeq = α • A
Besteht die Oberfläche eines Raumes – so wie dies meistens der Fall ist – aus verschiedenen Wandwerkstoffen, dann ergibt sich
Aeq = ∑ (αn • An)
n = Anzahl der Teilflächen
An = Teilfläche in m2
αn = Absorptionsgrad der Teilfläche
Die Nachhallzeit in Abhängigkeit von der äquivalenten Absorptionsfläche
Hört die akustische Erregung des Schallgebers auf, dann ist es nicht etwa so, dass das Schallfeld ebenfalls sofort verschwindet, es besteht noch ein Nachhall. Dabei ist es so, dass die noch vorhandene Schallenergie – nach einer exponentiellen Zeitfunktion – durch Absorption ,,verzehrt“ wird. Die dazu erforderliche Zeit ist die Nachhallzeit. Nach dem Vorschlag des französischen Akustikers W. C. Sabine (1868 bis 1919) ist international festgelegt:
Die Nachhallzeit ist die Zeit, innerhalb derer die Schallenergie (33) nach dem Aufhören eines Schallereignisses auf den 19-6 ten Teil des ursprünglichen Wertes bzw. der Schalldruckpegel Lp (62, 63, 66) um 60 dB gesunken ist.
Durch Versuche ist es Sabine gelungen, einen Zusammenhang zwischen der Nachhallzeit T, der äquivalenten Absorptionsfläche Aeq und dem Raumvolumen V zu finden. Die Gleichung, die diesen Sachverhalt beinhaltet, ist eine empirische Gleichung und man nennt sie die Sabine‘sche Nachhallgleichung. Es handelt sich dabei um eine Zahlenwertgleichung und lässt deshalb keine Einheitenrechnung zu. Daraus ergibt sich für die
Nachhallzeit T = 0,1635 • (V/Aeq)
V = Raumvolumen in m3
Aeq = äquivalante Absorptionsfläche in m2
Zur akustischen Beurteilung eines Raumes gibt es für die Nachhallzeit optimale Richtwerte, und zwar in Abhängigkeit vom Benutzungszweck. Diese sind schalltechnischen Handbüchern zu entnehmen und sind beim Bau von Akustikräumen zu beachten. Die folgende Tabelle zeigt einige Richtwerte:
Zusammenhang zwischen Schalldruck und Schallleistung
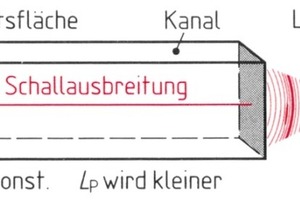
Bild 4 zeigt einen Lautsprecher, der elektrische Leistung in Schallleistung umwandelt und die vollkommen in einen Kanal eingeleitet wird:
Demzufolge kann diese Schallleistung in etwa als konstant in Schallausbreitungsrichtung angesehen werden. Sie ist eine theoretische, leicht berechenbare Größe. Mit konstanter Schallleistung ist auch der Schallleistungspegel LW = konst., und zwar ganz im Gegensatz zum Schalldruckpegel LP. Dieser wird bekanntlich mit zunehmender Entfernung von der Schallquelle kleiner. Somit gilt:
Der Schalldruck bzw. der Schalldruckpegel sind entfernungs- und raumabhängig, die Schallleistung und der Schallleistungspegel sind entfernungs- und raumunabhängig.
In dieser Entfernungs- und Raumunabhängigkeit der Schallleistung liegt ihr Wert als objektive Schallfeldgröße. Deshalb eignet sich die Schallleistung hervorragend als Ausgangsgröße aller schalltechnischen Berechnungen. Dies soll nun in den folgenden Punkten angewendet werden.
Richtungsfaktor beim
Schalleintritt in den Raum
In der Anordnung des Bildes 4 wird Schallenergie in Ausbreitungsrichtung durch einen Kanal geleitet, so dass an der Schallaustrittsfläche eine bestimmte vorhandene Schallleistung vorausgesetzt werden kann.Diese ist wegen der unvermeidlichen Verluste – z. B. beim Eintritt in den Kanal oder beim Strömen durch den Kanal – um einen bestimmten Betrag kleiner geworden als die Schallleistung beim Eintritt beträgt.
Über derartige Leistungsverluste wird noch ausführlich in Beitrag 68 gesprochen.
Wir gehen also beim Kanal in Bild 4 von einer bestimmten Austrittsleistung (an der Austrittsfläche) aus.
Mündet ein solcher Kanal in einen Raum ein, dann wird die Kanalaustrittsleistung zur Raumeintrittsleistung des Schalls.
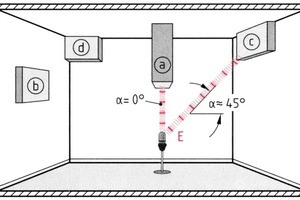
Gemäß Bild 5 legt man in der akustischen Messtechnik – bezogen auf den Schallempfänger E – die folgenden vier Mündungslagen fest:
Diese verschiedenen Mündungslagen bestimmen den sogenannten Richtungsfaktor Q. Dieser ist eine wichtige Rechengröße bei schalltechnischen Berechnungen, mit denen wir uns in den nächsten Beiträgen 68 und 69 beschäftigen wollen.
Bilder und Daten aus Horst Herr:
„Tabellenbuch Wärme· Kälte· Klima“
Verlag Europa-Lehrmittel (Nr. 1731 X)
„Schwingungen und Wellen“ (Nr. 5181 X)
„Technische Physik“ (Nr. 5231 X)
Dipl.-Ing. Horst Herr VDI, DKV ist Autor zahlreicher Lehrbücher sowie Formel- und Tabellensammlungen. Er ist ausgebildeter Berufsschullehrer und war viele Jahre als Dozent an der BFS Kälte-Klima-Technik in Maintal tätig. Wegen des hohen Stellenwertes der Physik in der Kälte- und Klimatechnik erklärt er in der KKA in jeder Ausgabe einen oder mehrere zusammengehörige Begriffe aus der Physik. Nach dem Motto „Was ist eigentlich...?“ werden in systematischer Abfolge physikalische Vorgänge und Begriffe erörtert bzw. aufgefrischt. Wir regen das Sammeln der Beiträge an, die deswegen durchgehend nummeriert werden.